2093: 2.12-97:[CF140E]New Year Garland
Time Limit: 5 Sec Memory Limit: 256 MB Submit: 0 Solved: 1[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
As Gerald, Alexander, Sergey and Gennady are already busy with the usual New Year chores, Edward hastily decorates the New Year Tree. And any decent New Year Tree must be decorated with a good garland. Edward has lamps of m colors and he wants to make a garland from them. That garland should represent a sequence whose length equals L. Edward's tree is n la
Edward adores all sorts of math puzzles, so he suddenly wondered: how many different ways to assemble the garland are there given that the both following two conditions are met:
Help Edward find the answer to this nagging problem or else he won't manage to decorate the Tree by New Year. You may consider that Edward has an unlimited number of lamps of each of m colors and it is not obligatory to use all m colors. The garlands are considered different if they differ in at least one position when represented as sequences. Calculate the answer modulo p. 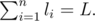
Input
The first line contains three integers n, m and p (1 ≤ n, m ≤ 106, 2 ≤ p ≤ 109) which are the number of the tree's la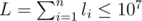 ).
).
Output
Sample Input Copy
3 2 1000
3 1 2
Sample Output Copy
8
HINT
输入:
2 3 1000
2 2
输出:
24
样例三:
输入:
1 1 1000
5
输出:
0
样例解释:
In the first sample the following variants are possible: 121|1|12, 121|1|21, 121|2|12, 121|2|21, 212|1|12, 212|1|21, 212|2|12, 212|2|21. In the second sample the following variants are possible: 12|13, 12|23, 12|31, 12|32 and so on.
Figure for the first sample:
